Frictionless experiment with a torsion balance apparatus
Using metrology similar
to Henry Cavendish’s 1706 experiment to measure the force of gravity between masses
If the idea/principle/method/law disagrees with the
experiment it’s wrong, that all there is to it (Richard Feynman
describing what science is).
Experiment we must

Fig 10
We need an
airtight structure (box), and we must turn on the propellers for x seconds at
different positions.
Position 1, near
the box’s opposite side.
Position 2, far
from the box’s opposite side.
If the resulting
force (which we can deduce by box’s change in position/velocity) is the same
regardless of the propellers position, I am wrong and will never
bring this idea up again.
If the resulting
force decreases as the distance increases, well that means we have a new method
of space propulsion.
The method has
been tested horizontally on ball bearings, dry ice plucks and floating on
water, however in order to eliminate the influence of friction I shall suggest
the following “test rig”
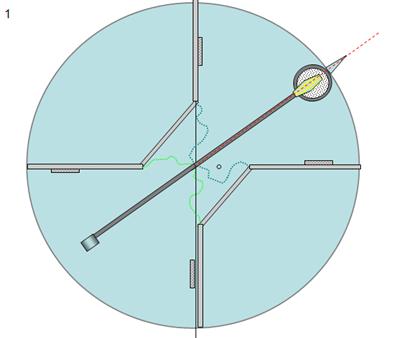
Simple Dynamic Tests Rig I.
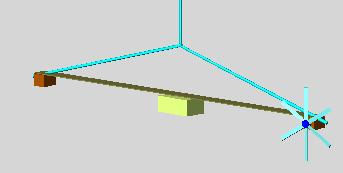
Fig 11
We put a motor and
propeller (representing mass M2) balanced by a counter weight hanging from a
string (Fig 11), this permits the assembly to easily rotate around the vertical
axis and will represent the movement of the inner free floating mass (M2).
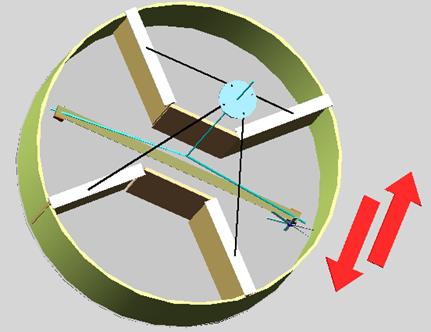
Fig 12
The balancing
motor assembly is inside a perimeter cylinder structure (fig 12), balancing motor assembly and perimeter cylinder structure
may rotate independently (until the balancing motor assembly bumps into the
separator borders).
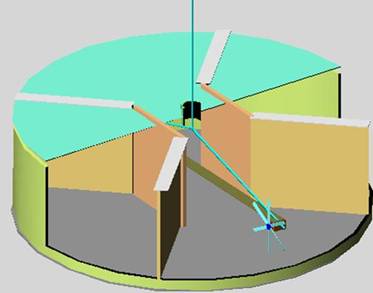
Fig 13
Cutaway (Fig 13)
illustrates the balancing motor can turn on its vertical axis independently of
the surrounding perimeter / support / separators for an approximately 40º angel
before colliding with one of the separators.
We can replace
the balancing propeller with a wheel in direct contact with the perimeter
cylinder as a control experiment (see Note 2)
Testing
Turning on the
motor/propeller near (almost touching) “rear” separator
(As in
position 1 fig 10)
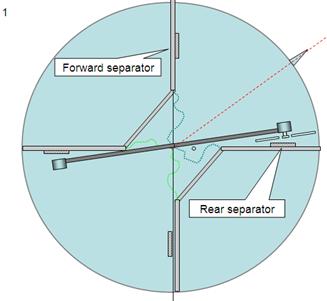
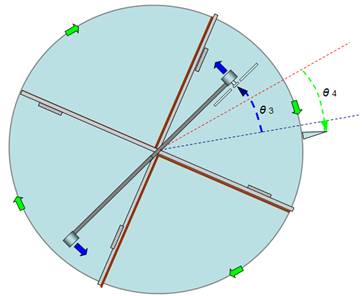
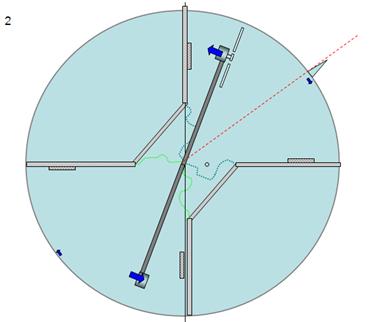
If we position
the motor/propeller assembly as close as possible to the “rear” separator (fig
14a), turning on the motor blows air directly against the “rear” separator
giving the perimeter cylinder a clockwise movement (green arrows), the
balancing motor/propeller assembly will accelerate in the counter clockwise
direction (blue arrows) (fig 14b) until it collides with the “forward”
separator bringing the perimeter cylinder’s clockwise spin to a standstill (fig
14c).
In the described
configuration it is difficult to obtain an increment in rotation of the
perimeter cylinder, the spacecraft will not accelerate.
Fig
14a Fig 14b
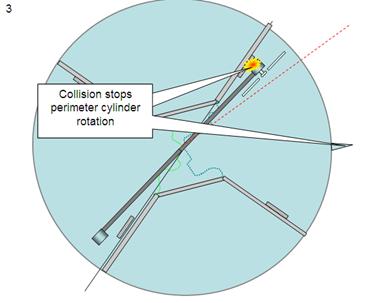
Fig 14c
Breakdown of results with motor/propeller near (almost touching)
the “rear” separator/target surface.
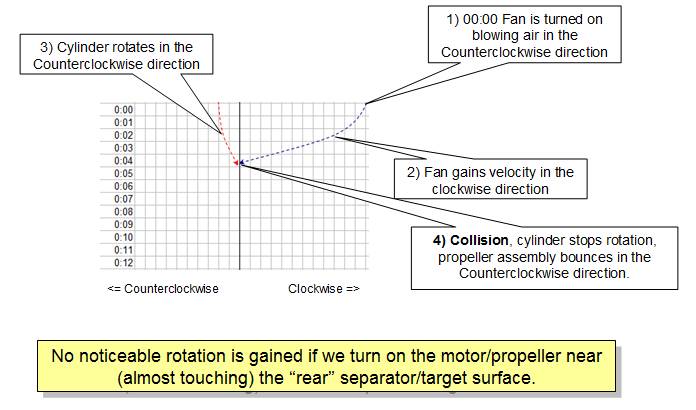
Fig 15
Turning on the
motor/propeller as far from the “rear” separator as is possible
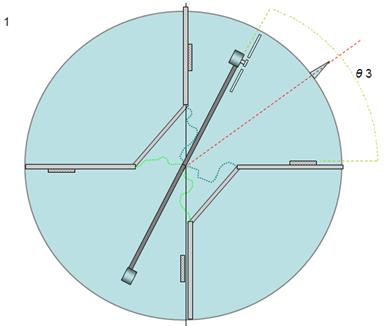
If we position
the balancing motor assembly’s initial position far form the “rear” separator
(fig 16a), with a approximate 35º angle (θ 3), when we turn on the
propeller the balancing motor assembly accelerates in the counter clockwise
direction (fig 16b) as in the previous experiment, but the perimeter cylinder’s
clockwise acceleration is significantly less than the previous experiment, this
is because the force exerted against an object by a (non laminar) gas flow is
inversely proportional to the distance separation gas source from the target
surface (separator) (see).
The instant of
collision between the balancing motor assembly and the “forward” separator (fig
16c) finds the perimeter cylinder has made only a small clockwise movement, and
the momentum transferred by the balancing motor assembly to the perimeter
cylinder is sufficient to accelerate it in the counter clockwise direction
beyond its original position and continue turning in the counter clockwise
direction (fig 16d).
By repeatedly
inverting the direction of the propeller (Note 3) it is
possible to continually “bump” the “forward” separator constantly increasing
the perimeter cylinders counterclockwise velocity. (See cycle for generation thrust on a
spacecraft)
Fig
16a Fig 16b
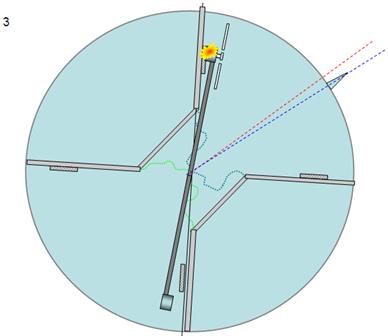
Fig
16c Fig 16d
Video
of the experiment II, another view
Breakdown of results with motor/propeller as far as possible from the “rear” separator/target
surface.
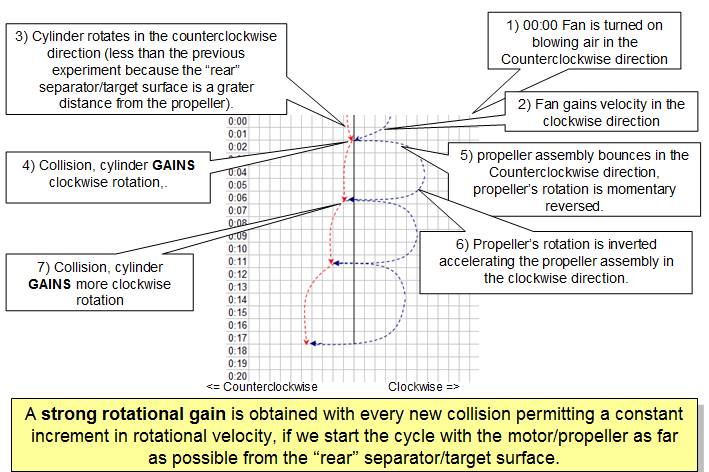
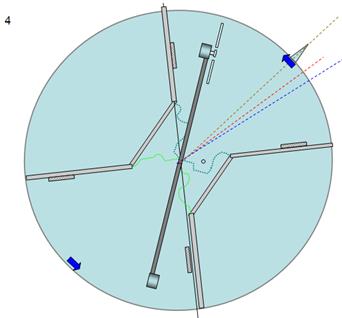
Fig 17
What is
observed?
When we turn on
the motor, the clockwise angular displacement of the perimeter cylinder is
depended on the distance that separate the propeller from the “rear” separator,
(Videos 1, 2 and 3), this is because the force exerted against an object by a
(non laminar) gas flow is inversely proportional to the distance separating gas
source from the target surface.
The balanced
motor assembly continues to gain angular velocity until it collides with one of
the separators (Fig 17c), it transfers momentum to the perimeter cylinder that gains velocity in the counter clock wise direction, the balanced
motor assembly bounces in the clockwise direction, the cycle can be repeated
indefinitely by changing the direction of the propeller (see Note 4) at the
appropriate moment (see videos 2 and 3)
Some are
disturbed because the experiment appears to contradict the law of conservation of linear momentum, others
that have given the matter some thought believe it does not.
Simple Dynamic Tests Rig II
Again I mention
that ideally the proposal should be tested in a micro gravity environment, as
the international space station is not available we constructed the test
assembly setup illustrated in fig 18.
A square aluminum
frame (2m) is attached by 4 cables to a long cord hung from the ceiling; this
setup permits the frame to rotate on its central axis with minimal friction.
On one end of the
aluminum frame we have a transparent airtight box (Fig 18) that will serve as
our closed system, at the opposite side a ballast (counter weight) for balance.
The assembly has freedom to rotate around the rotation axis.
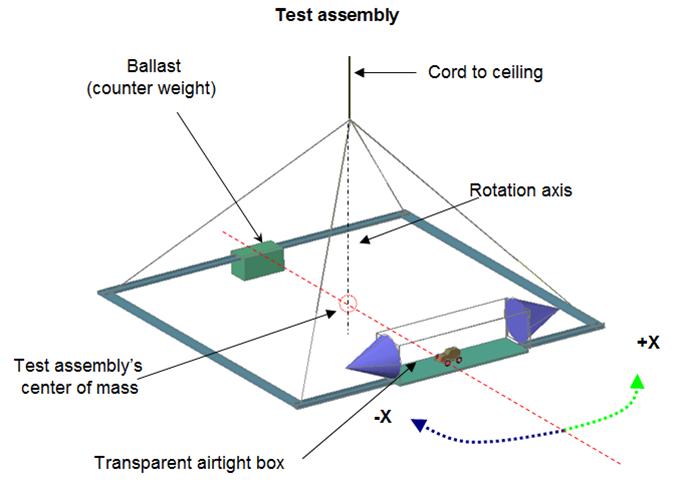
Fig 18

Fig 19
To illustrate the
effect a mass interacting inside a closed system (the transparent box), we will
first use a toy R/C car (Fig 19), when the toy car (internal mass) is turned on
it gains acceleration by directly interacting with the transparent box (fig
22).
Figs 20 and 21
show the toy car’s initial position at rest, at this moment all the elements on
the test bed are at rest.
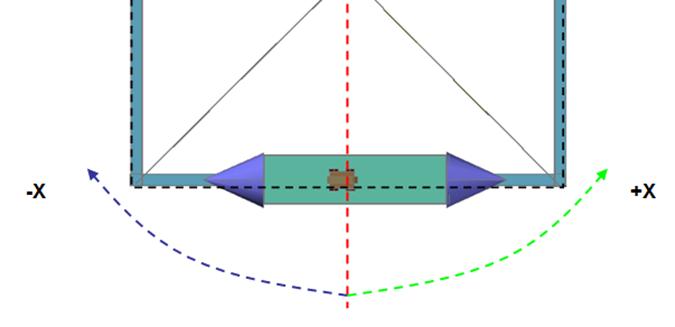
Fig 20
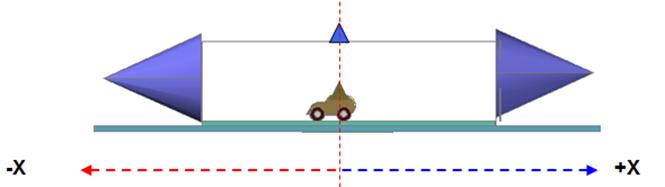
Fig 21
If we turn on the
car’s wheels in a counter clockwise direction, the car will move in the –X
direction and the transparent box moves in the +X direction making the frame
rotate in the counter clockwise or +X direction, fig 22 shows a side view of
the described actions, fig 23 shows a top view of the actions portrayed.
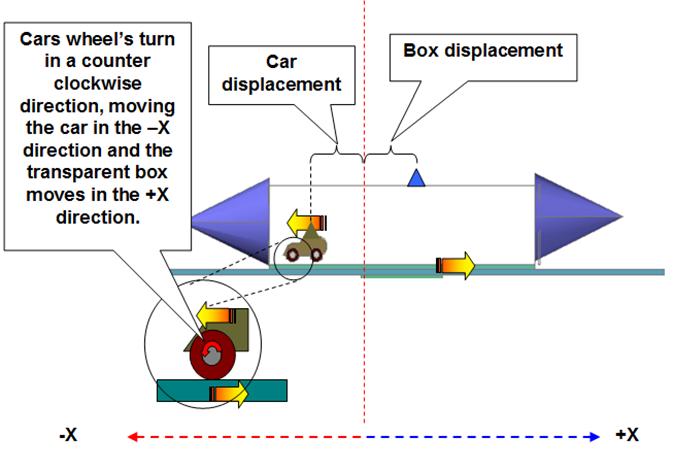
Fig 22
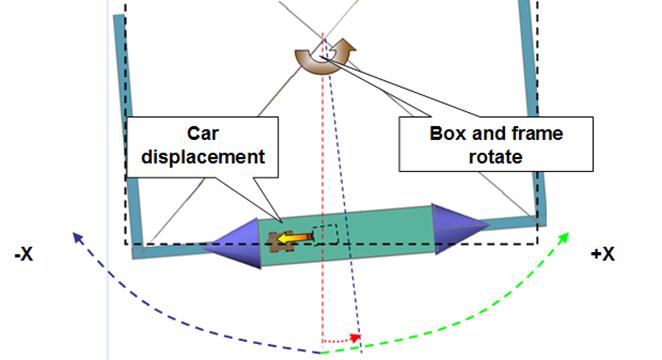
Fig 23
The frame will
continue to rotate in the +X direction until the car collides with the
transparent box’s inner –X surface (fig 24) exerting a force (F1), that cancels the frame’s rotation.
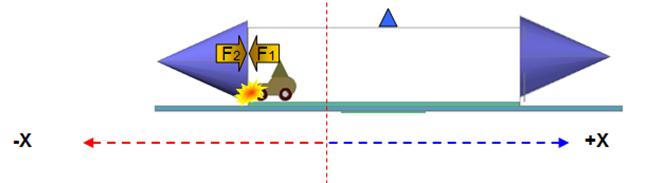
Fig 24
If we reverse the
toy car’s direction the objects will return to their original position. It is not possible to give the
frame a constant angular acceleration by any combination of movements we
command the toy car to perform, at
most we can obtain a cyclical clockwise/anticlockwise oscillation, but the
frame will not gain rotational velocity.
This so far
confirms that a closed system (spacecraft) cannot accelerate by
interaction/movements of masses inside the spacecraft if no mass is expelled
from the system.
Let’s do
something different
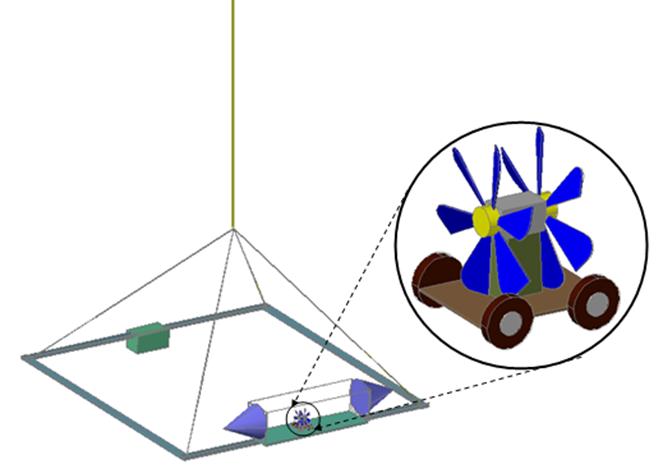
Fig 25
If we replace the
toy car with a propeller car (Fig 25), the wheels of the propeller car are
“free moving” and as frictionless as possible. If the propellers are turned on
the “car” is set in motion by the collision of air molecules and propeller.
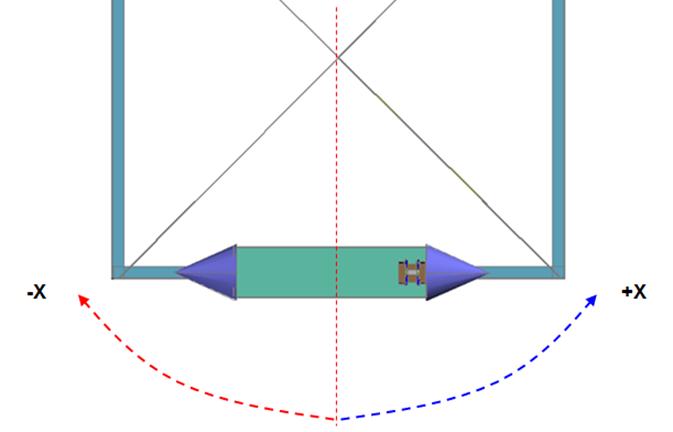
Fig 26
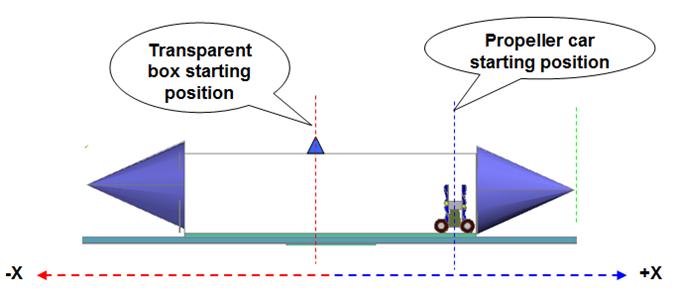
Fig 27
Figs 26 and 27
illustrate the test bed’s elements in their initial position at the start of
the experiment, the propeller
car is positioned against
the transparent box’s inner +X
side.
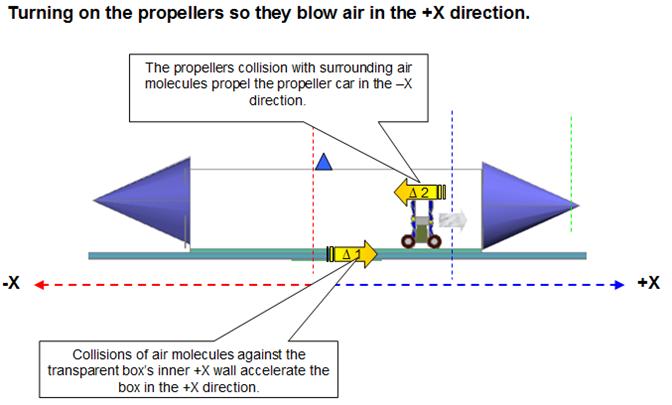
Fig 28
We will use
the R/C control to create a 3 part cycle (1-blow air in the +X direction,
2-blow air in the –X direction, 3-collition of car and box’s inner +X wall)
Part 1: We turn on the propellers so they blow air
in the +X direction against the transparent box’s inner +X side, this results in two actions: (Fig 28)
1-The propellers
collision with surrounding air molecules propel the propeller car in the –X
direction (fig 28 ∆2)
2-Collisions of
air molecules against the transparent box’s inner +X wall give the box a slight
acceleration in the +X direction (fig 28 ∆1) and the frame rotates
counter clock wise (fig 29).
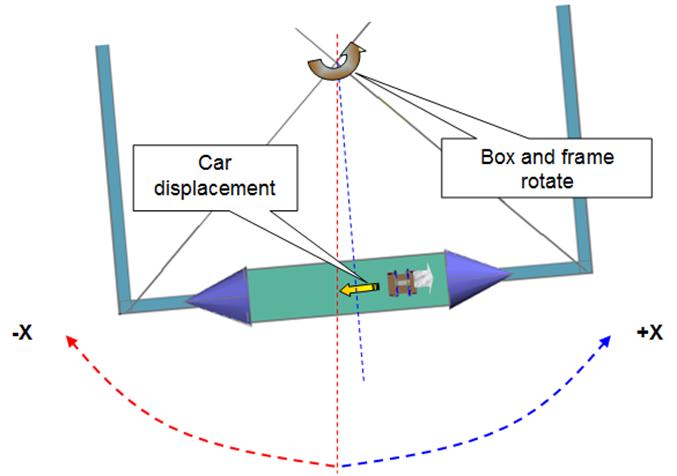
Fig 29
Part 2: As soon as the propeller car moves a few
centimeters in the –X direction, the propellers direction is inverted so that
air is blown in the –X direction, this makes the car change direction and
accelerate in the +X direction (figs 30 ∆ 3 and fig 31).
We observe that
although the frame’s counter clock wise rotation
slows slightly it does not stop (fig
31).
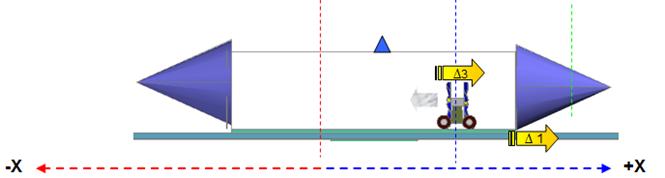
Fig 30
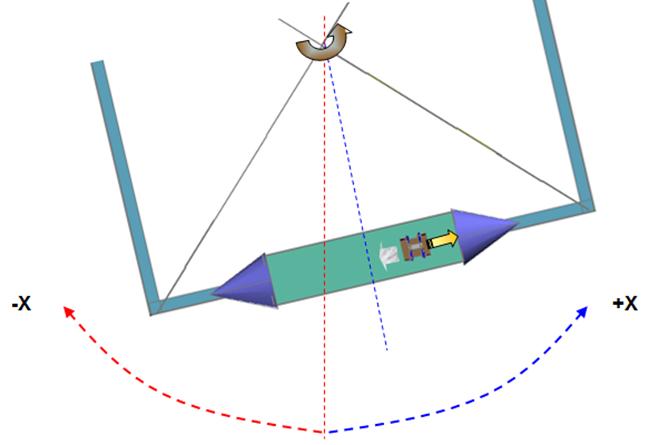
Fig 31
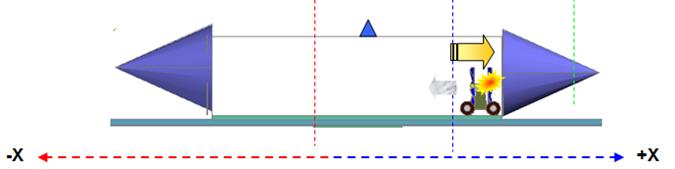
Fig 32
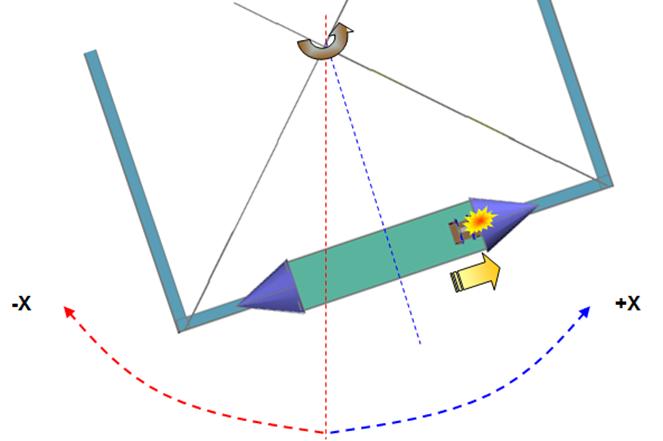
Fig 33
Part 3: the propeller car collides with the
transparent box’s inner +X (figs 32 and 33) giving a
hard “bump” that increments
the frame’s counter clock wise rotation velocity.
CONCLUSION
After repeating the experiment numerous times we can:
Confirm that it is not possible to increase the frame’s rotation
by acceleration of a contained mass by any means that requires direct contact
with the box (figs 20 to 24) (various other mechanisms were tried but not shown
in the document)
It is possible to increase the frame’s rotation if the contained
mass is made to accelerate with no direct contact with the cylinder by means of
air currents (figs 25 to 33).
This experiment is presented to observe a simple method of
propulsion for spacecraft and can be easily replicated.
No insights on apparent conflicts with the conservation of linear
momentum law are offered in this particular document.
Note 1 What about
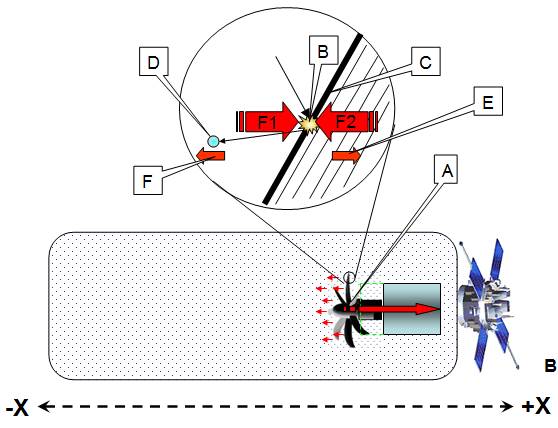
Fig 34
The motor spins
the propeller (A), when the propeller collides (B) with a air molecule (D) 2
equal and opposite forces interact, F1 pushes the propeller assembly in the +X
direction, and F2 hurls the molecule (D) in a –X direction.
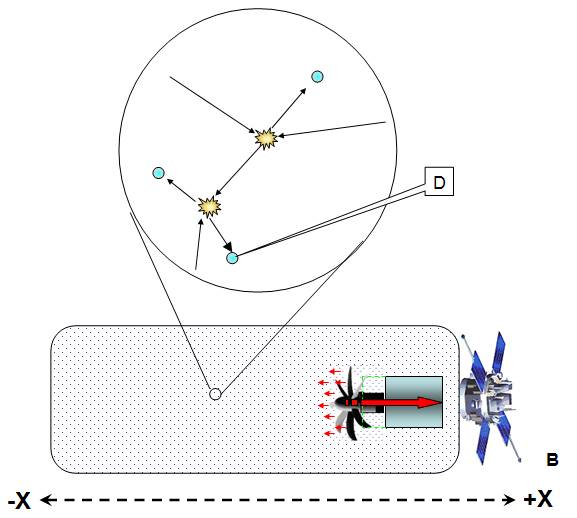
Fig 35
With every
collision (we are taking billions and billions of collisions) two equal forces
hurl the colliding molecules in different directions, the magnitude of the
forces does not change but the vector direction are randomized with every
collision. See kinetic
theory of gases.
Note 2 Control Experiment
|
a b |
36
If we attach the
wheeled assembly to the motor (b) in such a manner that the wheel is in contact
with the perimeter circle so that when the motor is turned on the wheel will
“roll” on the cylinder (Fig 36)
|
|
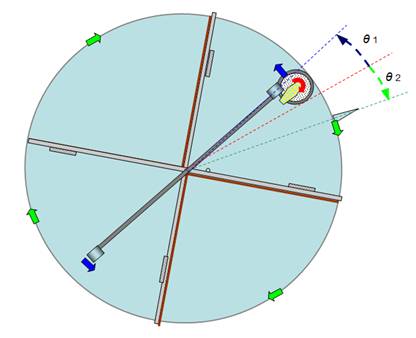
Fig
37a Fig
37b
Fig 37b
illustrates what happens when we turn on the motor so that the wheel turns in a
clockwise direction, the motor / wheel assembly pushing against the perimeter
cylinder will move in a counter clockwise direction (θ 1) while the perimeter cylinder will
turn in a clockwise direction (θ 2).
The ratio between
the counter clockwise angular displacement of the balancing motor assembly (θ 1) and the clockwise angular
displacement of the perimeter cylinder (θ 2) will depend on the ratio between the
masses of the objects, if they have equal mass (this can be controlled by
adding mass where necessary) the angular displacements will be equal. (Fig 37b)
If we reverse the
direction of the motor the objects will return to their original position. It
is not possible to give the perimeter cylinder a constant angular acceleration
if the balanced motor assembly is restrained to a fixed angle by separating
panels.
At most we can
obtain a cyclical clockwise anticlockwise oscillation
Note
3
To control the
propeller motor (on-off-left spin-right spin) it is best to use a RC controller
so that no external cables protrude from the assembly.
Suggested method:
Obtain an
inexpensive toy RC car or other toy
Remove the RC
circuit (generally includes the battery compartment) (fig 38)

Fig 38
Connect the control
wires of one of the toys motors (most have two or more) to the propeller motor,
in this example a normal LEGO motor (fig 12)
This setup will
control the propellers direction remotely.

Fig 39

