WJETech (we push from the inside)
Tecnologías William Jhon Elliott Somerville E.I.R.L.
Rut: 76722619-5
So how does this thing work again?
THIS PAGE IS A WORK IN PROGRESS
Videos of simple demonstration
model
NOTE:
The video shows a simple DIY model in a 6 liter water bottle, for our cubesat
under development we will use an aluminum cylinder (see)
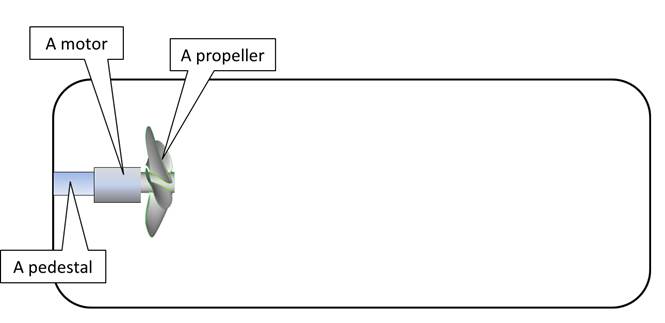
Fig 1
So we have our airtight bottle and inside is a motorized propeller, when we turn the motor on, the bottle moves. As basic physics clearly states that an object at rest cannot move UNLESS a force is applied to it, if no OUTSIDE force is applied then the force is INSIDE the bottle.
But basic physics also states that a closed system (airtight bottle) cannot push itself from the inside, it MUST expel mass (like a rocket), and yet we can clearly see in video 1 that the airtight bottle IS pushing itself from the inside.
Physics cannot have it both ways, here we have a conflict between our basic physics (law of conservation of linear momentum) and what we observe, someone is mistaken.
Here is where we remember what Richard Feynman said.
Let us take a closer look
inside the airtight container (the bottle), first we must remember that
although the bottle LOOKS empty to us, in
reality there are 15,18 x 10^25 molecules very fast moving molecules colliding
with each other in random manner (fig 2)

Fig 2
The fast moving molecules
collide with each other, with the inner walls of the bottle, with the elements
inside the bottle including the propeller.

For every collision there is a PUSH, but if you add the vector direction of all the molecules collisions the result will be 0 (not going anywhere)
When the propeller is activated it collides with billions of air molecules with a strong force sending them toward the rear of the bottle and interacting with billions and billions of molecules before affecting the rear of the bottle
To simplify we will take a look at the idealized interactions of ONE molecule (Fig 3).

Fig 3
When the propeller blade collides with the molecule it applies a strong force (F1) on the molecule, accelerating it towards the rear of the bottle (Fig 4).
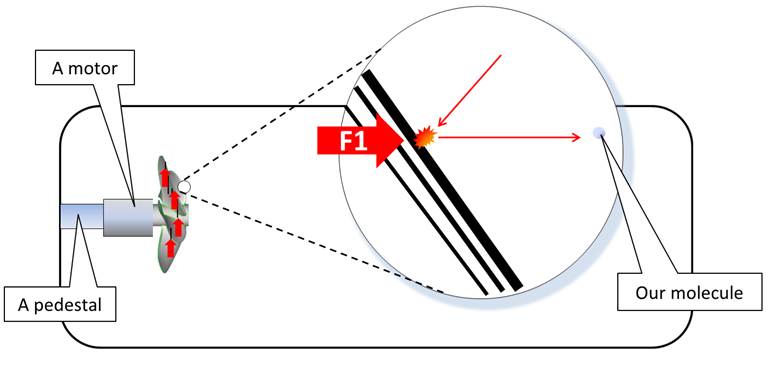
Fig 4
As for every action there is
an equal and opposite reaction the propeller blade receives a force (F2) that
pushes it (and the bottle) forward.

Note:
The Propeller, motor,
pedestal and bottle are SOLIDS (their molecules are BOUND), the air/gas inside
the bottle is composed of UNBOUND molecules.
So we can also view the
interactions inside the bottle as a pushing contest between BOUND and UNBOUND
molecules
BOUND
WINS.
Fig 5
As the molecule was
accelerated its momentum increases (momentum = velocity x mass) and it is
traveling with that momentum to the rear of the bottle (Fig. 6).

Fig. 6
If the molecule is very lucky
and it reaches the bottle’s rear wall without interacting with any of the 10^25
molecules inside the bottle (very lucky indeed) it will collide with the rear
inner wall with exactly the same force (F3) that the propeller received (F2),
the forces pushing the bottle forward (F2) and the force pushing the inner rear
end of the bottle (F3) are equal (Fig. 6)

Fig. 6
If every molecule that
collides with the propeller reaches the rear inner wall with its momentum
unchanged, the bottle will not move (Fig. 7)

Fig 7
But few molecules will get that lucky, most will collide with billions of molecules and their VECTOR DIRECTION will be randomized, many will not reach the rear inner wall with the same force.

Fig 7b
Also consider that the
propeller throws molecules outward and rapidly spinning against the cylinder’s
sides creating a vortex (Fig 7b) increasing the
molecular collisions against the side of the cylinder (also can be observed in
a cone shape)
Let’s take a closer look at two molecules colliding and how the collision affects their momentum.
Fig. 8 shows the first molecule 1 (M1) that is traveling towards the bottle’s rear inner wall, it has a mass (m1) and a velocity (v1)
Momentum is mass x velocity
therefore its momentum is m1 x v1 = p1

Fig. 8
Fig. 9 shows that molecule 1 is about to collide with incoming molecule 2 (M2) it has a mass (m2) and a velocity (v2)
Momentum is mass x velocity therefore its momentum is m2 x v2 = p2
If we add their momentum we
get p1 + p2 = p (f)
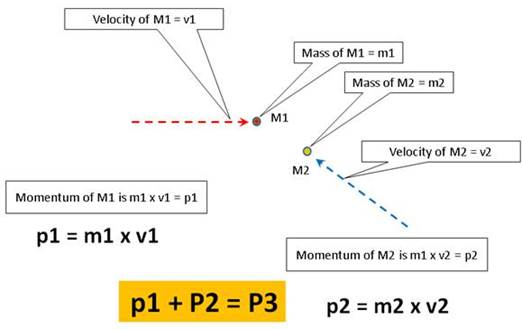
Fig. 9
If the two molecules collide
there are some changes (Fig. 10)
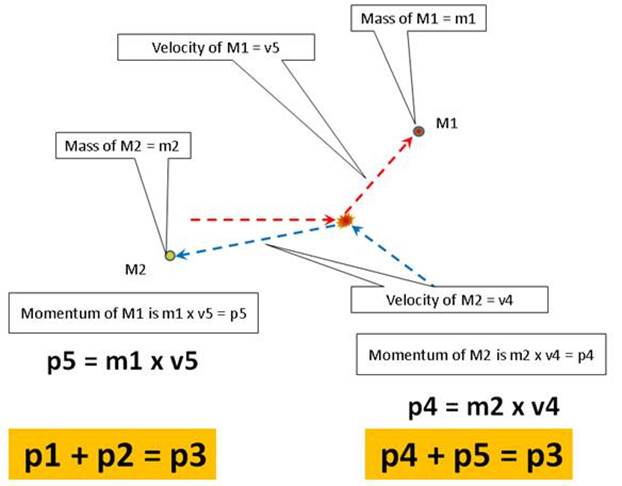
Fig. 10
|
Molecule 1 (M1) before collision |
Molecule 1 (M1) after collision |
|
Mass = m1 |
Mass = m1 (no change) |
|
Velocity = v1 |
Velocity may increase or decrease after the collision = v1(+ or -) |
|
Momentum = m1 x v1 = p1 |
Momentum = m1 x v1(+ or -) = p(a), the momentum of the individual molecule may change |
|
Molecule 2 (M2) before collision |
Molecule 2 (M2) after collision |
|
Mass = m2 |
Mass = m2 (no change) |
|
Velocity = v2 |
Velocity may increase or decrease after the collision = v2(+ or -) |
|
Momentum = m2 x v2 = p2 |
Momentum = m2 x v2(+ or -) = p(b), the momentum of the individual molecule may change |
|
Momentum of the SYSTEM (M1 + M2) before the collision |
Momentum of the SYSTEM (M1 + M2) after the collision |
|
p1 + p2 = p(s) |
p(a) + p(b) = p(s) |
|
Therefore: p1 + p2 = p(a) + p(b) = p(s) The momentum of the SYSTEM (both molecules) DOES NOT CHANGE |
|
Conclusion
The collision will not change the mass of the molecules
The collision may change the velocity of the molecules
The collision may change the momentum of individual molecules
The momentum of the system composed of both molecules does not change (in magnitude).
In order to describe momentum
its magnitude is not sufficient, we also need its direction, and we describe
its movement using a 3 axis graph (vector graph)
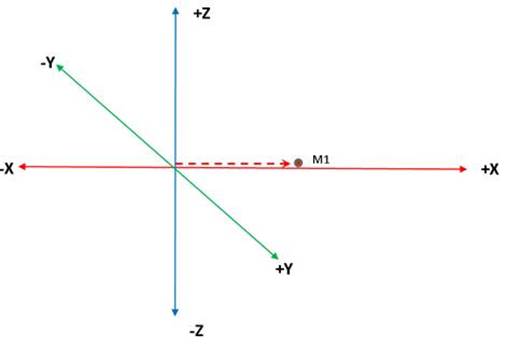
Fig 11
Fig 11 illustrates the vector
movement of molecule 1 (M1) it has a positive value in the X axis, 0 value in the Y and Z axis because it is moving straight
forward.
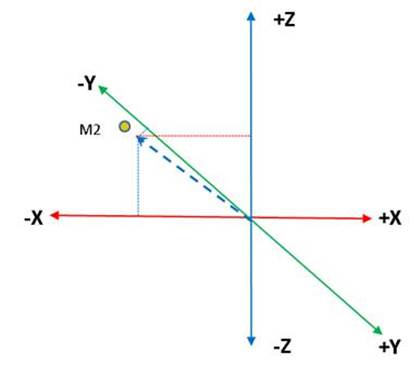
Fig 12
Fig 12 illustrates the
vector movement of molecule 2 (M2) it has a positive value in the Z axis (going
up), negative values in the X and Z axis, those values describe its vector
direction.
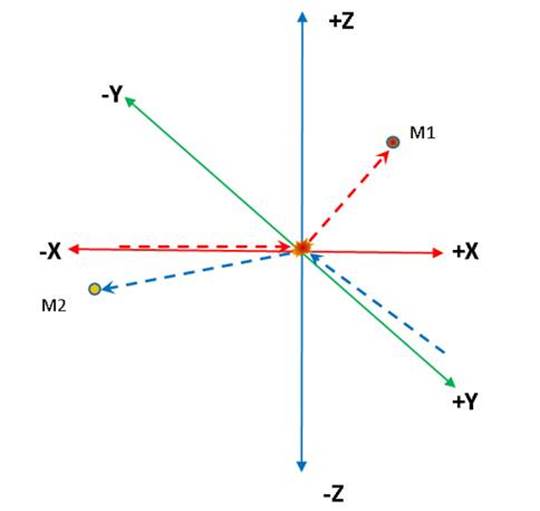
Fig 13
Fig 13 illustrates how the vectors of both molecules are changed, we have no way (that I know of) to predict the X, Y and Z values of each molecule, every collision will randomize their direction making it almost impossible that they reach the bottle’s rear end uninterrupted.